This blog collects some of my notes on classical computational learning theory, based on my reading of Kearns and Vazirani. The results are (almost) all from their book, the sloganising (and mistakes, no doubt) are mine.
The Probably Approximately Correct (PAC) Framework
Definition (Instance Space). An instance space is a set, typically denoted  . It is the set of objects we are trying to learn about.
. It is the set of objects we are trying to learn about.
Definition (Concept). A concept  over
over  is a subset of the instance space
is a subset of the instance space  .
.
Although not covered in Kearns and Vazirani, in general it is possible to generalise beyond Boolean membership to some degree of uncertainty or fuzziness – I hope to cover this in a future blog post.
Definition (Concept Class). A concept class  is a set of concepts, i.e.
is a set of concepts, i.e.  , where
, where  denotes power set. We will follow Kearns and Vazirani and also use
denotes power set. We will follow Kearns and Vazirani and also use  to denote the corresponding indicator function
to denote the corresponding indicator function  .
.
In PAC learning, we assume  is known, but the target class
is known, but the target class  is not. However, it doesn’t seem a jump to allow for unknown target class, in an appropriate approximation setting – I would welcome comments on established frameworks for this.
is not. However, it doesn’t seem a jump to allow for unknown target class, in an appropriate approximation setting – I would welcome comments on established frameworks for this.
Definition (Target Distribution). A target distribution  is a probability distribution over
is a probability distribution over  .
.
In PAC learning, we assume  is unknown.
is unknown.
Definition (Oracle). An oracle is a function  taking a concept class and a distribution, and returning a labelled example
taking a concept class and a distribution, and returning a labelled example  where
where  is drawn randomly and independently from
is drawn randomly and independently from  .
.
Definition (Error). The error of a hypothesis concept class  with reference to a target concept class
with reference to a target concept class  and target distribution
and target distribution  , is
, is  , where
, where  denotes probability.
denotes probability.
Definition (Representation Scheme). A representation scheme for a concept class  is a function
is a function  where
where  is a finite alphabet of symbols (or – following the Real RAM model – a finite alphabet augmented with real numbers).
is a finite alphabet of symbols (or – following the Real RAM model – a finite alphabet augmented with real numbers).
Definition (Representation Class). A representation class is a concept class together with a fixed representation scheme for that class.
Definition (Size). We associate a size  with each string from a representation alphabet
with each string from a representation alphabet  . We similarly associate a size with each concept
. We similarly associate a size with each concept  via the size of its minimal representation
via the size of its minimal representation  .
.
Definition (PAC Learnable). Let  and
and  be representation classes classes over
be representation classes classes over  , where
, where  . We say that concept class
. We say that concept class  is PAC learnable using hypothesis class
is PAC learnable using hypothesis class  if there exists an algorithm that, given access to an oracle, when learning any target concept
if there exists an algorithm that, given access to an oracle, when learning any target concept  over any distribution
over any distribution  on
on  , and for any given
, and for any given  and
and  , with probability at least
, with probability at least  , outputs a hypothesis
, outputs a hypothesis  with
with  .
.
Definition (Efficiently PAC Learnable). Let  and
and  be representation classes classes over
be representation classes classes over  , where
, where  for all
for all  . Let
. Let  or
or  . Let
. Let  ,
,  , and
, and  . We say that concept class
. We say that concept class  is efficiently PAC learnable using hypothesis class
is efficiently PAC learnable using hypothesis class  if there exists an algorithm that, given access to a constant time oracle, when learning any target concept
if there exists an algorithm that, given access to a constant time oracle, when learning any target concept  over any distribution
over any distribution 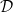 on
on  , and for any given
, and for any given  and
and  :
:
- Runs in time polynomial in
 ,
,  ,
,  , and
, and  , and
, and
- With probability at least
 , outputs a hypothesis
, outputs a hypothesis  with
with  .
.
There is much of interest to unpick in these definitions. Firstly, notice that we have defined a family of classes parameterised by dimension  , allowing us to talk in terms of asymptotic behaviour as dimensionality increases. Secondly, note the key parameters of PAC learnability:
, allowing us to talk in terms of asymptotic behaviour as dimensionality increases. Secondly, note the key parameters of PAC learnability: 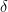 (the ‘probably’ bit) and
(the ‘probably’ bit) and  (the ‘approximate’ bit). The first of these captures the idea that we may get really unlucky with our calls to the oracle, and get misleading training data. The second captures the idea that we are not aiming for certainty in our final classification accuracy, some pre-defined tolerance is allowable. Thirdly, note the requirements of efficiency: polynomial scaling in dimension, in size of the concept (complex concepts can be harder to learn), in error rate (the more sloppy, the easier), and in probability of algorithm failure to find a suitable hypothesis (you need to pay for more certainty). Finally, and most intricately, notice the separation of concept class from hypothesis class. We require the hypothesis class to be at least as general, so the concept we’re trying to learn is actually one of the returnable hypotheses, but it can be strictly more general. This is to avoid the case where the restricted hypothesis classes are harder to learn; Kearns and Vazirani, following Pitt and Valiant, give the example of learning the concept class 3-DNF using the hypothesis class 3-DNF is intractable, yet learning the same concept class with the more general hypothesis class 3-CNF is efficiently PAC learnable.
(the ‘approximate’ bit). The first of these captures the idea that we may get really unlucky with our calls to the oracle, and get misleading training data. The second captures the idea that we are not aiming for certainty in our final classification accuracy, some pre-defined tolerance is allowable. Thirdly, note the requirements of efficiency: polynomial scaling in dimension, in size of the concept (complex concepts can be harder to learn), in error rate (the more sloppy, the easier), and in probability of algorithm failure to find a suitable hypothesis (you need to pay for more certainty). Finally, and most intricately, notice the separation of concept class from hypothesis class. We require the hypothesis class to be at least as general, so the concept we’re trying to learn is actually one of the returnable hypotheses, but it can be strictly more general. This is to avoid the case where the restricted hypothesis classes are harder to learn; Kearns and Vazirani, following Pitt and Valiant, give the example of learning the concept class 3-DNF using the hypothesis class 3-DNF is intractable, yet learning the same concept class with the more general hypothesis class 3-CNF is efficiently PAC learnable.
Occam’s Razor
Definition (Occam Algorithm). Let  and
and  be real constants. An algorithm is an
be real constants. An algorithm is an 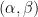 -Occam algorithm for
-Occam algorithm for  using
using  if, on an input sample
if, on an input sample  of cardinality
of cardinality  labelled by membership in
labelled by membership in  , the algorithm outputs a hypothesis
, the algorithm outputs a hypothesis  such that:
such that:
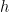 is consistent with
is consistent with  , i.e. there is no misclassification on
, i.e. there is no misclassification on 

Thus Occam algorithms produce succinct hypotheses consistent with data. Note that the size of the hypothesis is allowed to grow only mildly – if at all – with the size of the dataset (via 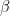 ). Note, however, that there is nothing in this definition that suggests predictive power on unseen samples.
). Note, however, that there is nothing in this definition that suggests predictive power on unseen samples.
Definition (Efficient Occam Algorithm). An 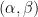 -Occam algorithm is efficient iff its running time is polynomial in
-Occam algorithm is efficient iff its running time is polynomial in  ,
,  , and
, and  .
.
Theorem (Occam’s Razor). Let  be an efficient
be an efficient 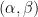 -Occam algorithm for
-Occam algorithm for  using
using  . Let
. Let  be the target distribution over
be the target distribution over  , let
, let  be the target concept,
be the target concept,  . Then there is a constant
. Then there is a constant  such that if
such that if  is given as input a random sample
is given as input a random sample  of
of  examples drawn from oracle
examples drawn from oracle  , where
, where  satisfies
satisfies  , then
, then  runs in time polynomial in
runs in time polynomial in  ,
,  ,
,  and
and  and, with probability at least
and, with probability at least  , the output
, the output 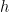 of
of  satisfies
satisfies  .
.
This is a technically dense presentation, but it’s a philosophically beautiful result. Let’s unpick it a bit, so its essence is not obscured by notation. In summary, simple rules that are consistent with prior observations have predictive power! The ‘simple’ part here comes from 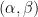 , and the predictive power comes from the bound on
, and the predictive power comes from the bound on  . Of course, one needs sufficient observations (the complex lower bound on
. Of course, one needs sufficient observations (the complex lower bound on  ) for this to hold. Notice that as
) for this to hold. Notice that as 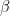 approaches 1, and so – by the definition of an Occam algorithm – we get close to being able to memorise our entire training set – we need an arbitrarily large training set (memorisation doesn’t generalise).
approaches 1, and so – by the definition of an Occam algorithm – we get close to being able to memorise our entire training set – we need an arbitrarily large training set (memorisation doesn’t generalise).
Vapnik-Chervonenkis (VC) Dimension
Definition (Behaviours). The set of behaviours on  that are realised by
that are realised by  , is defined by
, is defined by  .
.
Each of the points in  is either included in a given concept or not. Each tuple
is either included in a given concept or not. Each tuple  then forms a kind of fingerprint of
then forms a kind of fingerprint of  according to a particular concept. The set of behaviours is the set of all such fingerprints across the whole concept class..
according to a particular concept. The set of behaviours is the set of all such fingerprints across the whole concept class..
Definition (Shattered). A set  is shattered by
is shattered by  iff
iff  .
.
Note that  is the maximum cardinality that’s possible, i.e. the set of behaviours is all possible behaviours. So we can think of a set as being shattered by a concept class iff there’s no combination of inclusion/exclusion in the concepts that isn’t represented at least once in the set.
is the maximum cardinality that’s possible, i.e. the set of behaviours is all possible behaviours. So we can think of a set as being shattered by a concept class iff there’s no combination of inclusion/exclusion in the concepts that isn’t represented at least once in the set.
Definition (Vapnik-Chervonenkis Dimension). The VC dimension of  , denoted
, denoted  , is the cardinality of the largest set shattered by
, is the cardinality of the largest set shattered by  . If arbitrarily large finite sets can be shattered by
. If arbitrarily large finite sets can be shattered by  , then
, then  .
.
VC dimension in this sense captures the ability of  to discern between samples.
to discern between samples.
Theorem (PAC-learning in Low VC Dimension). Let  be any concept class. Let
be any concept class. Let  be any representation class off of VC dimension
be any representation class off of VC dimension  . Let
. Let  be any algorithm taking a set of
be any algorithm taking a set of  labelled examples of a concept
labelled examples of a concept  and producing a concept in
and producing a concept in  that is consistent with the examples. Then there exists a constant
that is consistent with the examples. Then there exists a constant 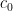 such that
such that  is a PAC learning algorithm for
is a PAC learning algorithm for  using
using  when it is given examples from
when it is given examples from  , and when
, and when  .
.
Let’s take a look at the similarity between this theorem and Occam’s razor, presented in the last section of this blog post. Both bounds have a similar feel, but the VCD-based bound does not depend on  ; indeed it’s possible that the size of hypotheses is infinite and yet the VCD is still finite.
; indeed it’s possible that the size of hypotheses is infinite and yet the VCD is still finite.
As the theorem below shows, the linear dependence on VCD achieved in the above theorem is actually the best one can do.
Theorem (PAC-learning Minimum Samples). Any algorithm for PAC-learning a concept class of VC dimension  must use
must use  examples in the worst case.
examples in the worst case.
Definition (Layered DAG). A layered DAG is a DAG in which each vertex is associated with a layer  and in which the edges are always from some layer
and in which the edges are always from some layer 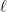 to the next layer
to the next layer 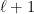 . Vertices at layer 0 have indegree 0 and are referred to as input nodes. Vertices at other layers are referred to as internal nodes. There is a single output node of outdegree 0.
. Vertices at layer 0 have indegree 0 and are referred to as input nodes. Vertices at other layers are referred to as internal nodes. There is a single output node of outdegree 0.
Definition ( -composition). For a layered DAG
-composition). For a layered DAG  and a concept class
and a concept class  , the G-composition of
, the G-composition of  is the class of all concepts that can be obtained by: (i) associating a concept
is the class of all concepts that can be obtained by: (i) associating a concept  with each vertex
with each vertex 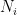 in
in  , (ii) applying the concept at each node to its predecessor nodes.
, (ii) applying the concept at each node to its predecessor nodes.
Notice that this way we can think of the internal nodes as forming a Boolean circuit with a single output; the  -composition is the concept class we obtain by restricting concepts to only those computable with the structure
-composition is the concept class we obtain by restricting concepts to only those computable with the structure  . This is a very natural way of composing concepts – so what kind of VCD arises through this composition? This theorem provides an answer:
. This is a very natural way of composing concepts – so what kind of VCD arises through this composition? This theorem provides an answer:
Theorem (VCD Compositional Bound). Let  be a layered DAG with
be a layered DAG with  input nodes and
input nodes and 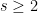 internal nodes, each of indegree
internal nodes, each of indegree  . Let
. Let  be a concept class over
be a concept class over  of VC dimension
of VC dimension  , and let
, and let  be the
be the  -composition of
-composition of  . Then
. Then  .
.
Weak PAC Learnability
Definition (Weak PAC Learning). Let  be a concept class and let
be a concept class and let  be an algorithm that is given access to
be an algorithm that is given access to  for target concept
for target concept  and distribution
and distribution 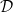 .
.  is a weak PAC learning algorithm for
is a weak PAC learning algorithm for  using
using  if there exist polynomials
if there exist polynomials  and
and  such that
such that  outputs a hypothesis
outputs a hypothesis  that with probability at least
that with probability at least  satisfies
satisfies  .
.
Kearns and Vazirani justifiably describe weak PAC learning as “the weakest demand we could place on an algorithm in the PAC setting without trivialising the problem”: if these were exponential rather than polynomial functions in  , the problem is trivial: take a fixed-size random sample of the concept and memorise it, randomly guess with probability 50% outside the memorised sample. The remarkable result is that efficient weak PAC learnability and efficient PAC learnability coincide for an appropriate PAC hypothesis class, based on ternary majority trees.
, the problem is trivial: take a fixed-size random sample of the concept and memorise it, randomly guess with probability 50% outside the memorised sample. The remarkable result is that efficient weak PAC learnability and efficient PAC learnability coincide for an appropriate PAC hypothesis class, based on ternary majority trees.
Definition (Ternary Majority Tree). A ternary majority tree with leaves from  is a tree where each non-leaf node computes a majority (voting) function of its three children, and each leaf is labelled with a hypothesis from
is a tree where each non-leaf node computes a majority (voting) function of its three children, and each leaf is labelled with a hypothesis from  .
.
Theorem (Weak PAC learnability is PAC learnability). Let  be any concept class and
be any concept class and  any hypothesis class. Then if
any hypothesis class. Then if  is efficiently weakly PAC learnable using
is efficiently weakly PAC learnable using  , it follows that
, it follows that  is efficiently PAC learnable using a hypothesis class of ternary majority trees with leaves from
is efficiently PAC learnable using a hypothesis class of ternary majority trees with leaves from  .
.
Kearns and Varzirani provide an algorithm to learn this way. The details are described in their book, but the basic principle is based on “boosting”, as developed in the lemma to follow.
Definition (Filtered Distributions). Given a distribution 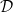 and a hypothesis
and a hypothesis 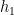 we define
we define  to be the distribution obtained by flipping a fair coin and, on a heads, drawing from
to be the distribution obtained by flipping a fair coin and, on a heads, drawing from  until
until 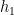 agrees with the label; on a tails, drawing from
agrees with the label; on a tails, drawing from  until
until 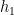 disagrees with the label. Invoking a weak learning algorithm on data from this new distribution yields a new hypothesis
disagrees with the label. Invoking a weak learning algorithm on data from this new distribution yields a new hypothesis 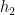 . Similarly, we define
. Similarly, we define  to be the distribution obtained by drawing examples from
to be the distribution obtained by drawing examples from  until we find an example on which
until we find an example on which 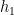 and
and 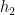 disagree.
disagree.
What’s going on in these constructions is quite clever: 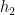 has been constructed so that it must contain new information about
has been constructed so that it must contain new information about  , compared to
, compared to 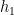 ;
; 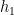 has, by construction, no advantage over a coin flip on
has, by construction, no advantage over a coin flip on  . Similarly,
. Similarly,  contains new information about
contains new information about  not already contained in
not already contained in 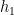 and
and 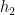 , namely on the points where they disagree. Thus, one would expect that hypotheses that work in these three cases could be combined to give us a better overall hypothesis. This is indeed the case, as the following lemma shows.
, namely on the points where they disagree. Thus, one would expect that hypotheses that work in these three cases could be combined to give us a better overall hypothesis. This is indeed the case, as the following lemma shows.
Lemma (Boosting). Let  . Let the distributions
. Let the distributions 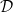 ,
,  ,
,  be defined above, and let
be defined above, and let 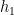 ,
, 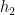 and
and  satisfy
satisfy  ,
,  ,
,  . Then if
. Then if  , it follows that
, it follows that  .
.
The function 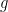 is monotone and strictly decreasing over
is monotone and strictly decreasing over  . Hence by combining three hypotheses with only marginally better accuracy than flipping a coin, the boosting lemma tells us that we can obtain a strictly stronger hypothesis. The algorithm for (strong) PAC learnability therefore involves recursively calling this boosting procedure, leading to the majority tree – based hypothesis class. Of course, one needs to show that the depth of the recursion is not too large and that we can sample from the filtered distributions with not too many calls to the overall oracle
. Hence by combining three hypotheses with only marginally better accuracy than flipping a coin, the boosting lemma tells us that we can obtain a strictly stronger hypothesis. The algorithm for (strong) PAC learnability therefore involves recursively calling this boosting procedure, leading to the majority tree – based hypothesis class. Of course, one needs to show that the depth of the recursion is not too large and that we can sample from the filtered distributions with not too many calls to the overall oracle  , so that the polynomial complexity bound in the PAC definition is maintained. Kearns and Vazirani include these two results in the book.
, so that the polynomial complexity bound in the PAC definition is maintained. Kearns and Vazirani include these two results in the book.
Learning from Noisy Data
Up until this point, we have only dealt with correctly classified training data. The introduction of a noisy oracle allows us to move beyond this limitation.
Definition (Noisy Oracle). A noisy oracle  extends the earlier idea of an oracle with an additional noise parameter
extends the earlier idea of an oracle with an additional noise parameter  . This oracle behaves in the identical way to
. This oracle behaves in the identical way to  except that it returns the wrong classification with probability
except that it returns the wrong classification with probability  .
.
Definition (PAC Learnable from Noisy Data). Let  be a concept class and let
be a concept class and let  be a representation class over
be a representation class over  . Then
. Then  is PAC learnable from noisy data using
is PAC learnable from noisy data using  if there exists and algorithm such that: for any concept
if there exists and algorithm such that: for any concept  , any distribution
, any distribution 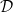 on
on  , any
, any  , and any
, and any  ,
,  and
and  with
with  , given access to a noisy oracle
, given access to a noisy oracle  and inputs
and inputs  ,
, 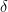 ,
,  , with probability at least
, with probability at least  the algorithm outputs a hypothesis concept
the algorithm outputs a hypothesis concept  with
with  . If the runtime of the algorithm is polynomial in
. If the runtime of the algorithm is polynomial in  ,
,  ,
,  and
and  then
then  is efficiently learnable from noisy data using
is efficiently learnable from noisy data using  .
.
Let’s unpick this definition a bit. The main difference from the PAC definition is simply the addition of noise via the oracle and an additional parameter  which bounds the error of the oracle; thus the algorithm is allowed to know in advance an upper bound on the noisiness of the data, and an efficient algorithm is allowed to take more time on more noisy data.
which bounds the error of the oracle; thus the algorithm is allowed to know in advance an upper bound on the noisiness of the data, and an efficient algorithm is allowed to take more time on more noisy data.
Kearns and Vazirani address PAC learnability from noisy data in an indirect way, via the use of a slightly different framework, introduced below.
Definition (Statistical Oracle). A statistical oracle  takes queries of the form
takes queries of the form  where
where  and
and  , and returns a value
, and returns a value  satisfying
satisfying  where
where ![P_\chi = Pr_{x \in {\mathcal D}}[ \chi(x, c(x)) = 1 ]](https://s0.wp.com/latex.php?latex=P_%5Cchi+%3D+Pr_%7Bx+%5Cin+%7B%5Cmathcal+D%7D%7D%5B+%5Cchi%28x%2C+c%28x%29%29+%3D+1+%5D&bg=ffffff&fg=000000&s=0&c=20201002) .
.
Definition (Learnable from Statistical Queries). Let  be a concept class and let
be a concept class and let  be a representation class over
be a representation class over  . Then
. Then  is efficiently learnable from statistical learning queries using
is efficiently learnable from statistical learning queries using  if there exists a learning algorithm
if there exists a learning algorithm  and polynomials
and polynomials  ,
,  and
and  such that: for any
such that: for any  , any distribution
, any distribution 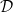 over
over  and any
and any  , if given access to
, if given access to  , the following hold. (i) For every query
, the following hold. (i) For every query  made by
made by  , the predicate
, the predicate  can be evaluated in time
can be evaluated in time  , and
, and  , (ii)
, (ii)  has execution time bounded by
has execution time bounded by  , (iii)
, (iii)  outputs a hypothesis
outputs a hypothesis  that satisfies
that satisfies  .
.
So a statistical oracle can be asked about a whole predicate  , for any given tolerance
, for any given tolerance  . The oracle must return an estimate of the probability that this predicate holds (where the probability is over the distribution over
. The oracle must return an estimate of the probability that this predicate holds (where the probability is over the distribution over  ). It is, perhaps, not entirely obvious how to relate this back to the more obvious noisy oracle used above. However, it is worth noting that one can construct a statistical oracle that works with high probability by taking enough samples from a standard oracle, and then returning the relative frequency of
). It is, perhaps, not entirely obvious how to relate this back to the more obvious noisy oracle used above. However, it is worth noting that one can construct a statistical oracle that works with high probability by taking enough samples from a standard oracle, and then returning the relative frequency of  evaluating to 1 on that sample. Kearns and Vazirani provide an intricate construction to efficiently sample from a noisy oracle to produce a statistical oracle with high probability. In essence, this then allows an algorithm that can learn from statistical queries to be used to learn from noisy data, resulting in the following theorem.
evaluating to 1 on that sample. Kearns and Vazirani provide an intricate construction to efficiently sample from a noisy oracle to produce a statistical oracle with high probability. In essence, this then allows an algorithm that can learn from statistical queries to be used to learn from noisy data, resulting in the following theorem.
Theorem (Learnable from Statistical Queries means Learnable from Noisy Data). Let  be a concept class and let
be a concept class and let  be a representation class over
be a representation class over  . Then if
. Then if  is efficiently learnable from statistical queries using
is efficiently learnable from statistical queries using  ,
,  is also efficiently PAC learnable using
is also efficiently PAC learnable using  in the presence of classification noise.
in the presence of classification noise.
Hardness Results
I mentioned earlier in this post that Pitt and Valiant showed that sometimes we want more general hypothesis classes than concept classes: the concept class 3-DNF using the hypothesis class 3-DNF is intractable, yet learning the same concept class with the more general hypothesis class 3-CNF is efficiently PAC learnable. So in their chapter Inherent Unpredictability, Kearns and Vazirani turn their attention to the case where a concept class is hard to learn independent of the choice of a hypothesis class. This leads to some quite profound results for those of us interested in Boolean circuits.
We will need some kind of hardness assumption to develop hardness results for learning. In particular, note that if  , then by Occam’s Razor (above) polynomially evaluable hypothesis classes are also polynomially-learnable ones. So we will need to do two things: focus our attention on polynomially evaluable hypothesis classes (or we can’t hope to learn them polynomially), and make a suitable hardness assumption. The latter requires a very brief detour into some results commonly associated with cryptography.
, then by Occam’s Razor (above) polynomially evaluable hypothesis classes are also polynomially-learnable ones. So we will need to do two things: focus our attention on polynomially evaluable hypothesis classes (or we can’t hope to learn them polynomially), and make a suitable hardness assumption. The latter requires a very brief detour into some results commonly associated with cryptography.
Let  . We define the cubing function
. We define the cubing function  by
by  . Let
. Let  define Euler’s totient function. Then if
define Euler’s totient function. Then if  is not a multiple of three, it turns out that
is not a multiple of three, it turns out that  is bijective, so we can talk of a unique discrete cube root.
is bijective, so we can talk of a unique discrete cube root.
Definition (Discrete Cube Root Problem). Let 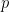 and
and 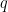 be two
be two  -bit primes with
-bit primes with  not a multiple of 3, where
not a multiple of 3, where 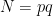 . Given
. Given  and
and 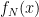 as input, output
as input, output  .
.
Definition (Discrete Cube Root Assumption). For every polynomial 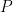 , there is no algorithm that runs in time
, there is no algorithm that runs in time 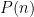 that solves the discrete cube root problem with probability at least
that solves the discrete cube root problem with probability at least  , where the probability is taken over randomisation of
, where the probability is taken over randomisation of 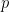 ,
, 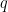 ,
,  and any internal randomisation of the algorithm
and any internal randomisation of the algorithm  . (Where
. (Where 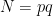 ).
).
This Discrete Cube Root Assumption is widely known and studied, and forms the basis of the learning complexity results presented by Kearns and Vazirani.
Theorem (Concepts Computed by Small, Shallow Boolean Circuits are Hard to Learn). Under the Discrete Cube Root Assumption, the representation class of polynomial-size, log-depth Boolean circuits is not efficiently PAC learnable (using any polynomially evaluable hypothesis class).
The result also holds if one removes the log-depth requirement, but this result shows that even by restricting ourselves to only log-depth circuits, hardness remains.
In case any of my blog readers knows: please contact me directly if you’re aware of any resource of positive results on learnability of any compositionally closed non-trivial restricted classes of Boolean circuits.
The construction used to provide the result above for Boolean circuits can be generalised to neural networks:
Theorem (Concepts Computed by Neural Networks are Hard to Learn). Under the Discrete Cube Root Assumption, there is a polynomial 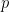 and an infinite family of directed acyclic graphs (neural network architectures)
and an infinite family of directed acyclic graphs (neural network architectures)  such that each
such that each  has
has 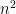 Boolean inputs and at most
Boolean inputs and at most  nodes, the depth of
nodes, the depth of  is a constant independent of
is a constant independent of  , but the representation class
, but the representation class  is not efficiently PAC learnable (using any polynomially evaluable hypothesis class), and even if the weights are restricted to be binary.
is not efficiently PAC learnable (using any polynomially evaluable hypothesis class), and even if the weights are restricted to be binary.
Through an appropriate natural definition of reduction in PAC learning, Kearns and Vazirani show that the PAC-learnability of all these classes reduce to functions computed by deterministic finite automata. So, in particular:
Theorem (Concepts Computed by Deterministic Finite Automata are Hard to Learn). Under the Discrete Cube Root Assumption, the representation class of Deterministic Finite Automata is not efficiently PAC learnable (using any polynomially evaluable hypothesis class).
It is this result that motivates the final chapter of the book.
Experimentation in Learning
As discussed above, PAC model utilises an oracle that returns labelled samples  . An interesting question is whether more learning power arises if we allow the algorithms to be able to select
. An interesting question is whether more learning power arises if we allow the algorithms to be able to select  themselves, with the oracle returning
themselves, with the oracle returning  , i.e. not just to be shown randomly selected examples but take charge and test their understanding of the concept.
, i.e. not just to be shown randomly selected examples but take charge and test their understanding of the concept.
Definition (Membership Query). A membership query oracle takes any instance  and returns its classification
and returns its classification  .
.
Definition (Equivalence Query). An equivalence query oracle takes a hypothesis concept  and determines whether there is an instance
and determines whether there is an instance  on which
on which  , returning this counterexample if so.
, returning this counterexample if so.
Definition (Learnable From Membership and Equivalence Queries). The representation class  is efficiently exactly learnable from membership and equivalence queries if there is a polynomial
is efficiently exactly learnable from membership and equivalence queries if there is a polynomial  and an algorithm with access to membership and equivalence oracles such that for any target concept
and an algorithm with access to membership and equivalence oracles such that for any target concept  , the algorithm outputs the concept
, the algorithm outputs the concept  in time
in time  .
.
There are a couple of things to note about this definition. It appears to be a much stronger requirement than PAC learning, as the concept must be exactly learnt. On the other hand, the existence of these more sophisticated oracles, especially the equivalence query oracle, appears to narrow the scope. Kearns and Vazirani encourage the reader to prove that the true strengthening over PAC-learnability is in the membership queries:
Theorem (Exact Learnability from Membership and Equivalence means PAC-learnable with only Membership). For any representation class  , if
, if  is efficiently exactly learnable from membership and equivalence queries, then
is efficiently exactly learnable from membership and equivalence queries, then  is also efficiently learnable in the PAC model with membership queries.
is also efficiently learnable in the PAC model with membership queries.
They then provide an explicit algorithm, based on these two new oracles, to efficiently exactly learn deterministic finite automata.
Theorem (Experiments Make Deterministic Finite Automata Efficiently Learnable). The representation class of Deterministic Finite Automata is efficiently exactly learnable from membership and equivalence queries.
Note the contrast with the hardness result of the previous section: through the addition of experimentation, we have gone from infeasible learnability to efficient learnability. Another very philosophically pleasing result.
whose coordinates are partitioned into blocks
.
is a vector of low-precision mantissas, and
is a scalar shared scaling factor.
need not be normalized, and in many formats their entries may have quite different magnitudes (for example in integer mantissa formats such as MXINT). However this does not change the geometry. The representation
is invariant to rescaling of
: multiplying
by any constant simply rescales
by the inverse factor. What matters for the approximation is therefore only the direction of
, i.e. the one-dimensional subspace it spans.
of a vector into its magnitude and direction, but applied locally within blocks.
points roughly in the same direction as the original block
, then scaling it appropriately produces a good approximation of that block.
is not chosen arbitrarily, but rather is the best possible scale for that block in the least squares sense, for whatever mantissa vector we choose, i.e.
. Then
is the orthogonal projection of
onto the line spanned by
.
.
.
, which we can think of as the fraction of the vector’s energy contained in block
; these add to 1 over the whole vector. Now we can state the result:
.
represent how much of the vector’s energy lies in each block. Blocks that contain very little energy contribute very little to the final direction. The important consequence is that direction errors do not accumulate catastrophically across blocks. Instead, the overall directional error simply depends on a weighted average of the block direction errors. In other words, if block number formats preserve the directions of individual blocks, they automatically preserve the direction of the entire vector.
, the approximation
with
chosen by least squares is the orthogonal projection of
onto the line spanned by
.
where
is orthogonal to
.
gives
.
.
.
.
, we obtain
.
.
.
, and writing
,
.
, we obtain
.